VAE

对于许多模态，我们可以将我们观察到的数据视为由相关的不可见的潜在变量表示或生成的，我们可以用随机变量 z 来表示。表达这个想法的最佳直觉是通过柏拉图的Allegory of the Cave. 在寓言中，一群人一生都被锁在一个洞穴里，只能看到火光前经过的不可见三维物体投射在他们面前墙上的二维阴影。对这些人来说，他们所观察到的一切实际上是由他们永远无法看到的高维抽象概念决定的。

Vanilla VAE

根据洞穴寓言，我们认为我们所见的数据$x$都是某些高级空间中的向量$z$的投影。直观上讲，我们在现实世界中遇到的物体也可能是某些更高级表示的函数；例如，这些表示可能包含诸如颜色、大小、形状等抽象属性。不同的$x$以不同的概率对应同一个$z$,同一个$x$也可能以不同的概率对应不同的$z$(如x=小狗，它可能对应z=四足动物或者z=毛茸茸的物体)，反过来同一个$z$也以不同的概率对应不同的$x$，不同的$z$以不同的概率对应一个$x$（如z=四足动物也可以对应x=小猫，z=毛茸茸的物体可能对应x=毛线球）。所以事实上，VAE是encoder和decoder都是在预测一个分布。

In short,数学上，我们可以将潜在变量和我们观察到的数据建模为联合分布p(x,z)。

这样建模有什么好处呢，这样就避免了传统AE所做的x与z的一一对应，使得在z的分布过于稀疏、不连续，从而采样出无意义的数据。并且为了便于采样，我们总是让$z$服从标准高维高斯分布。

接下来我们简单得介绍一下VAE：

• VAE是建模$P_{data}(x)$的生成模型。
• 训练时VAE就是一个encoder-z-decoder架构，推理时直接采样z然后生成图片。
• 隐变量z是多维标准高斯分布，不随训练而发生改变。
• encoder生成给定样本x后,z的近似后验高斯分布的$\mu$和$\sigma$（因为z的真实后验分布不可知，这里用另一个分布去近似，这个技术叫变分推断，也就是VAE名字的由来）。注意:生成后验分布只是为了更容易采样去估计重构项，并不是要重塑z的分布，z依然是标准高斯分布
• decoder就是接收一个z，生成给定z时的真实数据的概率分布。注：这里如果x展平后各维度都是连续的，就建模为各维度独立的高斯分布，然后decoder输出$\mu$和$\sigma$；如果是离散的就待用分类分布或者两点分布，输出每一维的概率。
• 训练过程：目标是最大化ELBO,分为重构项（给定z，样本x的对数似然）和正则项（近似后验分布和先验分布的reverse-KL散度），正则项有解析解；重构项通过重参数化和采样进行估计，具体来说是从标准正态分布中采样一个$\epsilon$,然后$z=\mu+\sigma*\epsilon$,输入decoder计算似然。

Hierarchical VAE

正如上面所说，观测数据可能是潜变量的投影，而潜变量可能又是更抽象的变量的投影，于是我们自然引出了分层的VAE，即HVAE。

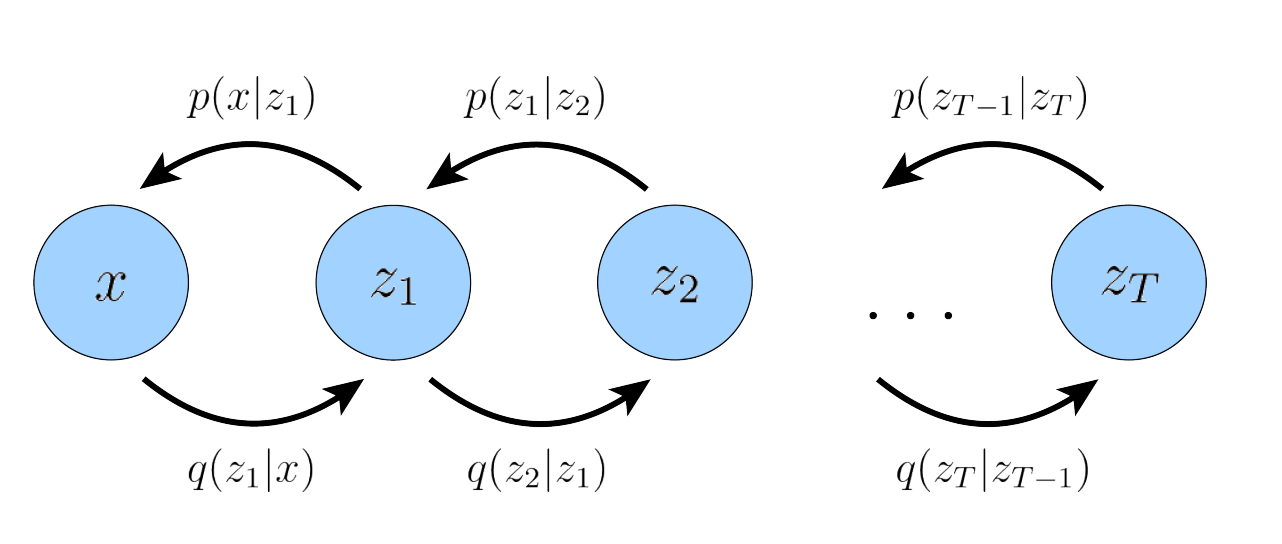
而在一般的具有 $T$ 层级的 HVAE 中，每个潜在变量都可以依赖于所有之前的潜在变量，在本文中我们关注一种特殊的案例，我们称之为马尔可夫 HVAE(MHVAE）。在 MHVAE 中，生成过程是一个马尔可夫链；也就是一个具有 $T$ 个层次潜在变量的马尔可夫链分层变分自编码器。生成过程被建模为一个马尔可夫链，其中每个潜在 $z_t$ 仅从之前的潜在 $z_{t+1}$ 生成。就是说，每一层向下的转移都是马尔可夫性的，其中解码每个潜在变量 $z_t$ 仅依赖于前一个潜在变量 $z_{t+1}$ 。

为什么要分层？ 我目前认为如果只有一层隐变量，被信息被压缩得太过厉害，我们很难训练一个能很好恢复的解码器。而分成很多层也许能允许我们更细粒度地从隐变量分布恢复出真实分布

一些自己瞎搞的数学推导

各维独立的多维分布的KL散度等于各维KL散度的和

Proof.

其中,$J$为随机向量$z$的维度，第二个等号是由于各维度相互独立，第四个等号是由于,当p(x)为概率密度函数时$\int_x p(x) dx=1$

原文中这个结论可以由积分的线性性质直接得到，但我不是很懂，故而自己用笨办法推导了一下。

为什么最大化观测数据的似然就是最大化ELBO

参考

参考链接