Wander's Whisper

--'Just do something，give destiny a reason to stir.'

Diffusion

Diffusion

Wander's avatar
Wander Tuesday, October 14, 2025

DDPM

这里省略了大量的数学推导，仅保留必要的数学表达式，以提高可读性

书接上回，我们可以认为variable diffusion model就是具有如下三条假设的HVAE:

  • 潜在维度恰好等于数据维度
  • 每个时间步的潜在编码器结构不是学成的；它是作为线性高斯模型预先定义的。换句话说，它是一个 以前一时间步输出为中心的高斯分布。
  • 潜在编码器的高斯参数随时间变化，使得最终时间步T 的潜在分布为标准正态分布

编码器

编码器显式地建模为: q(xt∣xt−1)=N(xt;αtxt−1,(1−αt)I)q\left(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{t-1}\right)=\mathcal{N}\left(\boldsymbol{x}_{t} ; \sqrt{\alpha_{t}} \boldsymbol{x}_{t-1},\left(1-\alpha_{t}\right) \mathbf{I}\right) 这称为线性高斯模型。

编码器这样规定的目的是：当我们任意给定一个干净图像x0x_0,我们总可以通过设置噪声调度并且在足够长的时间步T（这也是其推理很慢的原因）后使得xTx_T服从标准正态，进而方便我们进行采样。

并且，它有一些十分良好的性质，当我们给定了α1,α2,…,αT\alpha_1,\alpha_2,\dots,\alpha_T之后，q(xt∣x0)q(\boldsymbol{x}_t \mid \boldsymbol{x}_0)和q(xt−1∣xt,x0)q(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0)可以直接解析得到，且都是正态分布。

其中，q(xt∣x0)∼N(αtˉx0,(1−αtˉ)I),αtˉ=∏i=1tαiq(\boldsymbol{x}_t\mid\boldsymbol{x}_0)\sim \mathcal{N}(\sqrt{\bar{\alpha_t}}\boldsymbol{x_0},(1-\bar{\alpha_t})\mathbf{I}),\bar{\alpha_t}=\prod_{i=1}^t\alpha_i 另一个在下文给出。

ELBO

我们通过最大似然估计来优化模型参数，具体来说是通过优化似然函数的下界（ELBO）来间接优化似然函数。

表达式为：

log⁡p(x0)=∫log⁡p(x0:T)dx1:T\log{p(x_0)}=\int \log{p(x_{0:T})} dx_{1:T}

这表示了任意干净图像x0x_0的似然,对所有从正态分布到x0x_0的轨迹积分。

ELBO为:

Eq(x1∣x0)[log⁡pθ(x0∣x1)]⏟reconstruction term −DKL(q(xT∣x0)∥p(xT))⏟prior matching term −∑t=2TEq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))]⏟denoising matching term \underbrace{\mathbb{E}_{q\left(\boldsymbol{x}_{1} \mid \boldsymbol{x}_{0}\right)}\left[\log p_{\theta}\left(\boldsymbol{x}_{0} \mid \boldsymbol{x}_{1}\right)\right]}_{\text {reconstruction term }}-\underbrace{D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_{T} \mid \boldsymbol{x}_{0}\right) \| p\left(\boldsymbol{x}_{T}\right)\right)}_{\text {prior matching term }}-\sum_{t=2}^{T} \underbrace{\mathbb{E}_{q\left(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{0}\right)}\left[D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_{t}, \boldsymbol{x}_{0}\right) \| p_{\theta}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_{t}\right)\right)\right]}_{\text {denoising matching term }}

  1. Eq(x1∣x0)[log⁡pθ(x0∣x1)]\mathbb{E}_{q(\boldsymbol{x}_{1}|\boldsymbol{x}_{0})}\left[\log p_{\theta}(\boldsymbol{x}_{0}|\boldsymbol{x}_{1})\right] 可以解释为一个重构项；类似于普通VAE的ELBO中的对应项，这一项可以使用蒙特卡罗估计进行近似和优化。

  2. DKL(q(xT∣x0)∥p(xT))D_{\mathrm{KL}}(q(\boldsymbol{x}_{T}|\boldsymbol{x}_{0})\parallel p(\boldsymbol{x}_{T})) 表示最终加噪输入的分布与标准高斯先验的接近程度。它没有可训练参数，并且在我们的假设下也等于零。

  3. Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))]\mathbb{E}_{q(\boldsymbol{x}_{t}|\boldsymbol{x}_{0})}\left[D_{\mathrm{KL}}(q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t},\boldsymbol{x}_{0})\parallel p_{\theta}(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}))\right] 是一个降噪匹配项。我们学习期望的降噪转移步骤 pθ(xt−1∣xt)p_{\theta}(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}) 作为对易处理的、真实降噪转移步骤 q(xt−1∣xt,x0)q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t},\boldsymbol{x}_{0}) 的近似。q(xt−1∣xt,x0)q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t},\boldsymbol{x}_{0}) 转移步骤可以作为真实信号，因为它定义了如何在知道最终完全降噪图像 x0\boldsymbol{x}_{0} 应该是什么

其中，第一项的计算和VAE中的差不多，第二项是没有训练参数且T足够大时为0，计算量主要是第三项。根据线性高斯模型的性质可知，q(xt−1∣xt,x0)q(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t,\boldsymbol{x}_0)有解析式，且解析式为：

q(xt−1∣xt,x0)=N(xt−1;αt(1−αˉt−1)xt+αˉt−1(1−αt)x01−αˉt⏟μq(xt,x0),(1−αt)(1−αˉt−1)1−αˉtI)q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) = \mathcal{N}\left(\boldsymbol{x}_{t-1}; \underbrace{\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)\boldsymbol{x}_t + \sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_t\right)\boldsymbol{x}_0}{1-\bar{\alpha}_t}}_{\mu_q(\boldsymbol{x}_t, \boldsymbol{x}_0)}, \frac{\left(1-\alpha_t\right)\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t}\mathbf{I}\right)

由于协方差矩阵是常数且我们想要pθ(xt−1∣xt)p_\theta (\boldsymbol{x}_{t-1}\mid \boldsymbol{x}_t)与其尽可能接近，于是我们也把pθ(xt−1∣xt)p_\theta(\boldsymbol{x}_{t-1}\mid \boldsymbol{x}_t)建模为正态分布,且协方差矩阵与其相同。

再代入正态分布KL散度的公式，最后的优化目标为：

∣∣μθ−μq∣∣22||\mu_\theta-\mu_q||_2^2

即两者均值的L2距离的平方。 由于μθ\mu_\theta为xt\boldsymbol{x}_t和tt的函数，而并不是x0x_0的函数（这也就是为什么我们不可能直接解析地得到pθp_\theta的原因），为了与μq\mu_q尽量接近，我们将其建模为

μθ(xt,t)=αt(1−αˉt−1)xt+αˉt−1(1−αt)x^θ(xt,t)1−αˉt\mu_{\theta}\left(\boldsymbol{x}_{t}, t\right)=\frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right)\boldsymbol{x}_{t}+\sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_{t}\right)\hat{\boldsymbol{x}}_{\theta}\left(\boldsymbol{x}_{t}, t\right)}{1-\bar{\alpha}_{t}}

于是最后的的优化目标变成了

∥x^θ(xt,t)−x0∥22\left\|\hat{\boldsymbol{x}}_{\theta}\left(\boldsymbol{x}_{t}, t\right)-\boldsymbol{x}_{0}\right\|_{2}^{2}

因此，优化一个VDM归结为学习一个神经网络，从任意噪声化的版本中预测原始真实值图像。（为什么这个结论看起来是如此平凡🤣）此外，通过在所有噪声级别上最小化我们推导出的ELBO目标的第三项可以近似为在所有时间步上最小化期望（这是蒙特卡洛采样积分法，不得不说要不是有这种采样法，推导的这么一长串东西都完全没法算啊）：

arg⁡min⁡θ Et∼U{2,T}[Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))]]\underset{\boldsymbol{\theta}}{\arg\min}\,\mathbb{E}_{t \sim U\{2,T\}}\left[\mathbb{E}_{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}\left[D_{\mathrm{KL}}\left(q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \parallel p_{\boldsymbol{\theta}}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)\right)\right]\right]

然后可以使用随机样本在时间步上进行优化。

另外两种视角

而事实上这个目标函数还有另外两种等效的形式

第二种

首先，我们可以利用重参数化技巧。在推导 q(xt∣x0)q(\boldsymbol{x}_{t}|\boldsymbol{x}_{0}) 的形式时，我们可以重新排列方程来证明：

x0=xt−1−αˉtϵ0αˉt\boldsymbol{x}_{0} = \frac{\boldsymbol{x}_{t} - \sqrt{1-\bar{\alpha}_{t}}\boldsymbol{\epsilon}_{0}}{\sqrt{\bar{\alpha}_{t}}}

于是μq(xt,x0)\mu_q(\boldsymbol{x}_t,\boldsymbol{x}_0)可重新推导为：

μq(xt,x0)=1αtxt−1−αt1−αˉtαtϵ0\mu_q(\boldsymbol{x}_t,\boldsymbol{x}_0)=\frac{1}{\sqrt{\alpha_{t}}}\boldsymbol{x}_{t} - \frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}\sqrt{\alpha_{t}}}\boldsymbol{\epsilon}_{0}

因此，我们可以将我们的近似降噪转移均值 μθ(xt,t)\mu_{\theta}(\boldsymbol{x}_{t},t) 设置为：

μθ(xt,t)=1αtxt−1−αt1−αˉtαtϵ^θ(xt,t)\mu_{\theta}(\boldsymbol{x}_{t},t) = \frac{1}{\sqrt{\alpha_{t}}}\boldsymbol{x}_{t} - \frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}\sqrt{\alpha_{t}}}\hat{\boldsymbol{\epsilon}}_{\theta}(\boldsymbol{x}_{t},t)

并且相应的最优化问题变为：

arg⁡min⁡θ 12σq2(t)(1−αt)2(1−αˉt)αt[∥ϵ0−ϵ^θ(xt,t)∥22]\underset{\boldsymbol{\theta}}{\arg\min}\,\frac{1}{2\sigma_{q}^{2}(t)}\frac{\left(1-\alpha_{t}\right)^{2}}{\left(1-\bar{\alpha}_{t}\right)\alpha_{t}}\left[\left\|\boldsymbol{\epsilon}_{0}-\hat{\boldsymbol{\epsilon}}_{\theta}\left(\boldsymbol{x}_{t}, t\right)\right\|_{2}^{2}\right]

在这里，ϵ^θ(xt,t)\hat{\bm{\epsilon}}_{\theta}(\bm{x}_{t}, t)是一个神经网络，它学习预测决定xt\bm{x}_{t}的源噪声ϵ0∼N(ϵ;0,I)\bm{\epsilon}_{0} \sim \mathcal{N}(\bm{\epsilon}; \mathbf{0}, \mathbf{I})，从x0\bm{x}_{0}。因此，我们已经证明，通过预测原始图像x0\bm{x}_{0}来学习VDM等同于学习预测噪声；然而，实证研究表明，预测噪声取得了更好的性能。

这里也可以这样理解，任意时间步的图像都可以由原始图像一步加噪得到，我们只要用网络去预测加的那个噪声也可以达到同样的效果。并且也许预测噪声相当于resnet预测残差的想法，可能更容易拟合（？）故而效果更好。

而这实际上就是DDPM的做法。 ddpm

第三种

一个基于score-function的理解，可以看这个视频理解一下大概的思想。（这是视频实在对入门者相当的友好！）

这个解释可以通过Tweedie公式得到：

Tweedie公式指出，给定从指数族分布中抽取的样本，该分布的真实均值可以通过样本的极大似然估计（即经验均值）加上一个涉及估计得分的校正项来估计。在仅有一个观测样本的情况下，经验均值就是该样本本身。它常用于减轻样本偏差；如果观测样本都位于潜在分布的一端，那么负得分会变得很大，并将样本的朴素极大似然估计向真实均值进行修正。

数学上，对于高斯变量 z∼N(z;μz,Σz)z \sim \mathcal{N}(z; \mu_z, \Sigma_z)，Tweedie 公式表述为：

E[μz∣z]=z+Σz∇zlog⁡p(z)\mathbb{E}[\mu_z \mid z] = z + \Sigma_z \nabla_z \log p(z)

最后经过一系列推导我们可以发现，最后训练目标也可以归结为预测在任意时间步T下，q(xt∣x0)关于xtq(x_t|x_0)关于x_t的梯度。

并且，预测score function事实上和预测ϵ\epsilon只差了一个常数缩放因子。直观上，由于源噪声被添加到自然图像中以使其失真，因此向相反方向移动可以“去噪”图像，并且是提高后续对数概率的最佳更新。所以学习建模评分函数等同于建模源噪声的负数（忽略一个缩放因子）。

条件生成

参考这个视频，现在主流的方法是classifier-free guidance，大概的想法就是： 在推理（生成）时，我们不需要任何外部分类器。对于同一个输入噪声，我们让这个统一的模型同时进行两次预测：

  • 无条件预测：εuncond=model(xt,∅)ε_{uncond} = model(x_t, ∅)
  • 条件预测：εcond=model(xt,y)ε_{cond} = model(x_t, y)

然后，我们计算两者的方向差，并将这个差值放大： εfinal=εuncond+s∗(εcond−εuncond)ε_{final} = ε_{uncond} + s * (ε_{cond} - ε_{uncond})

DDIM

参考苏神博客 DDIM是是DDPM在的推广，它观察到DDPM的ELBO的推导中并未用到马尔可夫性质，故而取消了这一限制，只要求新的转移方式仍然满足原来的p(xt∣x0)p(x_t|x_0)，并且注意到当取消了马尔可夫性质后，q(xt−1∣xt,x0)q(x_{t-1}|x_t,x_0)不再是原来的表达式，我们可以通过推导得到其可以具备以下形式：

q(xt−1∣xt,x0)∼N(xt−1; βt−12−σt2βˉtxt+(αˉt−1−αˉt⋅βt−12−σt2βˉt)x0, σt2I)q(x_{t-1} \mid x_t, x_0) \sim \mathcal{N} \left( x_{t-1};\ \frac{\sqrt{\beta_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t} x_t + \left( \bar{\alpha}_{t-1} - \bar{\alpha}_t \cdot \frac{\sqrt{\beta_{t-1}^2 - \sigma_t^2}}{\bar{\beta}_t} \right) x_0,\ \sigma_t^2 \mathbf{I} \right)

其中σt\sigma_t可以自己设置，取某个值的时候会退化为DDPM，取0时,会变成确定性采样

进行上述改动后，事实上DDIM的训练算法和DDPM完全相同，区别只在采样。

而DDIM对于采样的加速取决于另一个观察：DDPM的训练结果实质上包含了它的任意子序列参数的训练结果。

所以实际上DDPM也可以进行跳步采样，而DDIM在此基础上更进一步，通过改变σt\sigma_t能得到更好的采样效果。

根据实验结果，应该是σt\sigma_t越小。效果越好。

下面给出σt\sigma_t取某一个值的时候的采样算法。

1. 选择时间步

  • 从集合 {1, …, T} 中选择一个包含 N 个时间步的子序列
S={s1,s2,...,sN},s1=1,  sN=T,  si<si+1 S = \{s_1, s_2, ..., s_N\}, \quad s_1 = 1, \; s_N = T, \; s_i < s_{i+1}
  • 记作
S={t0,t1,...,tN},tN=T,  t0=0S = \{t_0, t_1, ..., t_N\}, \quad t_N = T, \; t_0 = 0

2. 获取噪声预测模型

训练一个模型 ϵθ(xt,t)\epsilon_\theta(x_t, t) 来预测噪声 ϵ\epsilon，满足：

xt=αt x0+1−αt ϵ,ϵ∼N(0,I)x_t = \sqrt{\alpha_t} \, x_0 + \sqrt{1 - \alpha_t} \, \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)

3. 采样过程

  • 初始化：
xT∼N(0,I) x_T \sim \mathcal{N}(0, I)

  • 对于 i=N,...,1i = N, ..., 1：

    1. 预测噪声
    ϵ=ϵθ(xti,ti) \epsilon = \epsilon_\theta(x_{t_i}, t_i)
    1. 估计 x0x_0
    x^0=xti−1−αti ϵθ(xti,ti)αti \hat{x}_0 = \frac{x_{t_i} - \sqrt{1 - \alpha_{t_i}} \, \epsilon_\theta(x_{t_i}, t_i)}{\sqrt{\alpha_{t_i}}}
    1. 计算 σt\sigma_t 和均值 μt\mu_t
      （注意这里的αt\alpha_t并不是训练时所指定的那些）
    σt=η⋅1−αti−11−αti⋅1−αtiαti−1\sigma_t = \eta \cdot \sqrt{\frac{1 - \alpha_{t_{i-1}}}{1 - \alpha_{t_i}}} \cdot \sqrt{1 - \frac{\alpha_{t_i}}{\alpha_{t_{i-1}}}} μt=αti−1 x^0+1−αti−1−σt2 ϵθ(xti,ti) \mu_t = \sqrt{\alpha_{t_{i-1}}} \, \hat{x}_0 + \sqrt{1 - \alpha_{t_{i-1}} - \sigma_t^2} \, \epsilon_\theta(x_{t_i}, t_i)
    1. 更新采样
    xti−1∼N(μt,σt2)x_{t_{i-1}} \sim \mathcal{N}(\mu_t, \sigma_t^2)

    （当设定 η=0\eta = 0 时，σt\sigma_t = 0）

4. 输出

最终输出 x0x_0，即为生成的样本。

说明

  • αt\alpha_t：根据预定义的时间步 tt 计算的超参数，通常是线性或余弦调度函数。
  • ϵθ\epsilon_\theta：训练好的噪声预测模型。
  • x^0\hat{x}_0：对原始样本的估计值。
  • σt\sigma_t：控制采样过程中的随机性。
  • μt\mu_t：生成下一个时间步的均值。

DiT

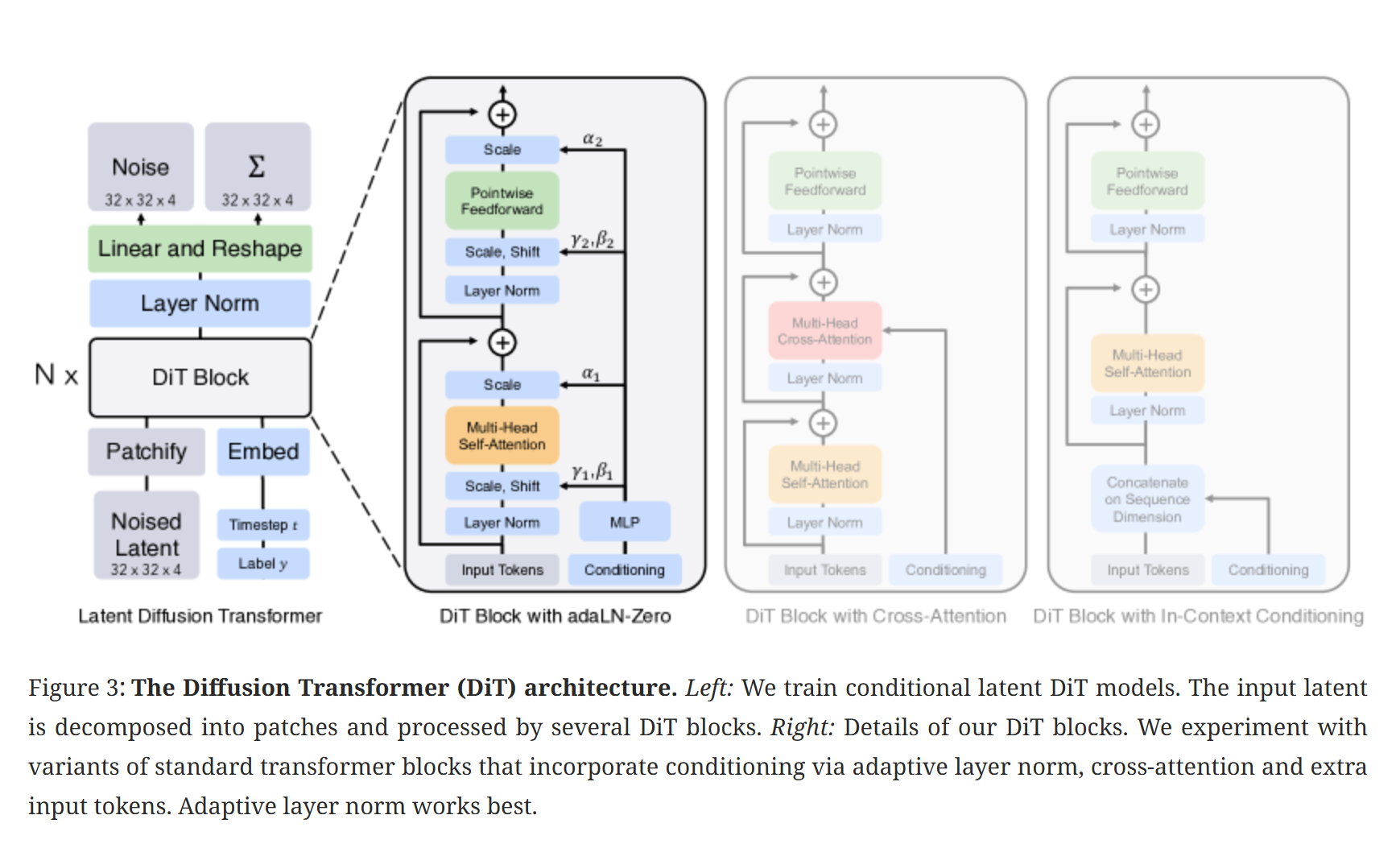用transformer架构替代了Unet，作为diffusion使用的架构。 DiT 这张图已然说明一切。

参考资料


Wander's avatar
Wander

Xjtu 24级计试，目前在研究具身智能相关话题~



Suggest changes on GitHub